Complete Summary of Absolute, Relative and Rotary Position Embeddings!
Position embeddings have been used a lot in recent LLMs. In this article, I explore the concept behind them and discuss the different types of position embeddings and their differences.
What are Position Embeddings?
In RNNs, the hidden state gets updated using the current state and past timestamps. However, transformers don’t naturally grasp the order of a sentence.
This is because the attention mechanism calculates relationships between tokens, with each token paying attention to all others in the sequence, without considering their order.
This means both of these sentences are the same to a transformer
Or any combination of those words.
To address this, researchers suggested ways to introduce the idea of order. They’re called position embeddings. So, position embeddings are vectors that we add to token embeddings to include information about order. An example of position embeddings introduced in the transformers paper is Absolute Embeddings.
What are Absolute Positional Embeddings?
Absolute embeddings are vectors with the same dimension as the word itself. This vector shows the word’s position in a sentence. Each word gets a unique absolute embedding to show its position in the sentence.
Then, we add the word embeddings with the token embeddings to give position information and feed them to the transformer.
How do we obtain these absolute embeddings?
There are two main ways you can create these embeddings.
Learn from data: You simply treat the position embeddings as weight parameters. Each position we learn a different vector embedding. This is bounded by the maximum length chosen.
Sinusoidal functions: Here we attempt to use mathematical functions that given a position in a sentence, this function will return a vector that encodes information about the position. In the original transformer paper we alternate between sine and cosine functions in the same dimension as the the word embedding. As you go higher in the position, the frequencies oscillate quicker.
With these functions, we can make special vector embeddings for each position. Both methods, learning from data and using sinusoidal functions, show the same performance based on experiments.
The Disadvantages of Absolute Positional Embeddings
The issue with absolute embeddings is that the transformer just remembers the position vectors, and we don’t give information about relative positions.
This means that to the model, position 1 and 2 look the same as position 1 and 500. There’s no pattern for the model to learn in the absolute embeddings.
Another problem is that positional embeddings struggle to predict positions they didn’t see during training.
For example, during training, if the sentences were only 512 tokens long, and then we get a longer sequence, we can make a positional embedding for token 520 and add it to the token embedding. However, since the model hasn’t seen this embedding before, it will struggle to adjust to it.
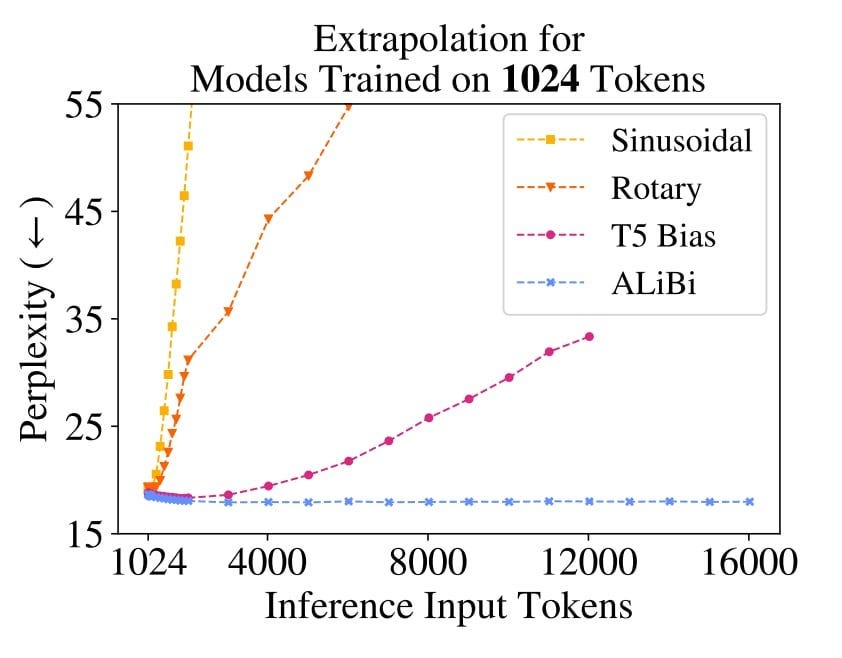
The figure above shows how the perplexity change as we increase the number of inference tokens, as you can see the sinusoidal embeddings skyrocket as we pass 512 tokens, rotary and T5 variant seem to perform better but ALiBi is the best which we will discuss in another article.
What Are Relative Positional Embeddings?
Instead of showing each token individually in a positional embedding, relative positional embeddings propose that we represent every pair of tokens in the sentence. This helps us understand the positions of tokens in relation to each other.
Since relative positional embeddings are calculated between two vectors, we can’t just add them directly to the token vector. Instead, they’re added directly to the self-attention mechanism.
First, we create a matrix that shows the distance between these tokens. The matrix looks like this.

We add the weight we compute the values matrix, so the following equation transforms into
this.
We also like to inform the self attention computation with the position information.
so we also add the position information to the query keys multiplication so
we transform it from the equation above to the equation below
In the relative positional encoding paper, they also use the concept of clipping. For instance, after many tokens, you might not want to calculate new position values; instead, you want to reuse values from tokens earlier.
To be specific, the relationship between token 1 and 499 probably won’t change much between token 1 and 500.
The parameter K, which indicates when to start clipping, is a hyperparameter that you can choose. This method works for long sequences and solves the problems we faced before, but it also has its drawbacks.
The Disadvantages of Relative Positional Embeddings
Because relative positional embeddings add new information that needs to be included in two spots during attention computation, it also causes additional delay during both training and inferences.

The images you see above are from the paper TRAIN SHORT, TEST LONG, where the authors compare various positional embedding methods. The T5 Bias variant uses relative positional embeddings.
We notice that relative positional embeddings are slower than other types of embeddings both during inference and training.
Another downside is that whenever we add a new token, we need to compute new key-value pairs, which means we can’t cache them.
What Are Rotary Positional Embeddings?
Instead of adding a positional embedding to the token embedding, the concept is to maintain the same embedding but rotate it by an angle θ. If a token is much further in a sentence, we rotate it by an integer multiplied by θ, with that integer showing the position in the sentence.
When we add tokens at the beginning or end, the angle between two tokens stays the same, thus preserving relative information.
For the 2D case, this equation applies the rotation:

The first matrix is the one that applies the rotation.
The last vector is the one we’re trying to rotate. Notice how we first do the key and query multiplication. This is because we aim to keep the same value even after changing the value ‘m’ that rotates the resulting vector.
For cases where we have more than 2D, we use the following equation.

Since our rotation matrix operates only on a 2D scale, we then split the vector to work with smaller sets of two values at a time, and then we rotate them.
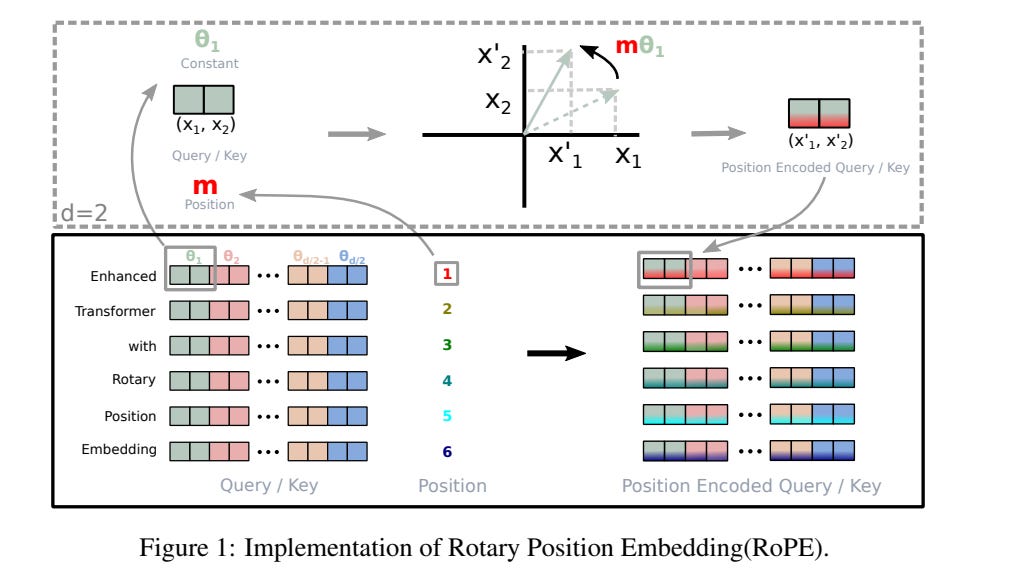
For the token enhanced, ‘m’ remains the same for every pair of weight values, but the angle θ changes for every two dimensions.
Because the rotation matrix is sparse, we can leverage that to create a much faster computation of the vectors following the equation below:
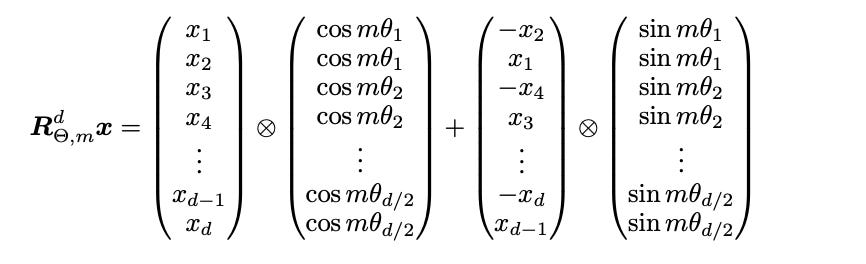
Results
The following figure demonstrates how RoPE embeddings prioritize tokens that are nearby, and this importance diminishes gradually as the relative distance increases, which is desirable.


The results indicate that RoFormer performs slightly better (only by 0.2) than the regular transformer on the translation task. This improvement is minor, so it could possibly be due to factors other than RoPE embeddings.

RoFormer appears to do better than the BERT variant on certain tasks but worse on others. This indicates that RoPE embeddings don’t necessarily outperform other types of embeddings for all tasks.

Looking at the figure above, we notice that transformer variants with RoPE embeddings reach convergence with fewer training steps compared to those without these embeddings.
Takeaways
The transformer doesn’t know the order of tokens in a sequence, so it needs position embeddings.
Absolute embeddings assign unique values to each token using learned weights or sinusoidal functions. However, the transformer can’t generalize using them when we go beyond the training sequence length.
Relative embeddings create a matrix that calculates weights for distances between tokens, and they are added directly to the attention mechanism. However, they are unable to cache keys and values, which makes the training and inference process slower.
Rotary embeddings rotate the token embedding by an angle depending on its position in the sequence. They can converge faster and generalize to long sequences. However, they don’t necessarily outperform all other embeddings on all tasks.
Papers And Resources
Self-Attention with Relative Position Representations
Relying entirely on an attention mechanism, the Transformer introduced by Vaswani et al. (2017) achieves…arxiv.org
https://arxiv.org/abs/2108.12409
https://arxiv.org/abs/2104.09864
Feel free to clap, follow, and comment if you enjoyed the article!
Stay In touch by connecting via LinkedIn Aziz Belaweid or GitHub.












